IR-> IR^3
u -> C(u) = a0 +a1.u +a2.u^2 + … + an.u^n = Somme_[i=0...n](ai.u^i)
Notez que le paramètre u prend des valeurs réelles, tandis que les coefficients ai sont des points de l’espace IR^3.
Si le degré n est grand, le temps de calcul de C(u) sera important,
c'est pourquoi on s'intéresse au cas particulier des courbes polynomiales
de degré 3, les cubiques. L'expression est alors :
C(u) = a0 +a1.u +a2.u^2 + a3.u^3
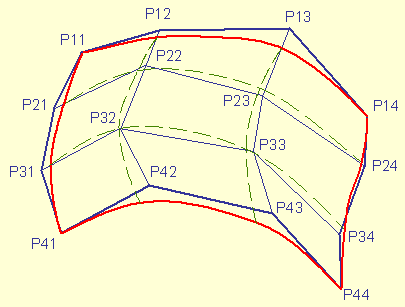
Voici en rouge et vert la représentation d’une courbe polynomiale
cubique étant donnés 4 points ai= (xi, yi, zi). La portion de
courbe en vert correspond à l'intervalle [0,1].
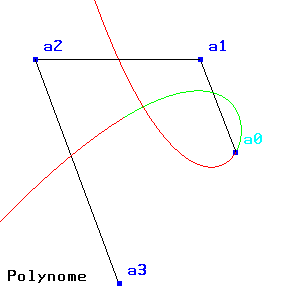 On remarque
que pour u=0, C=a0, mais dehors de cette propriété, les points
ai n’ont pas de signification géométrique particulière...
On remarque
que pour u=0, C=a0, mais dehors de cette propriété, les points
ai n’ont pas de signification géométrique particulière...
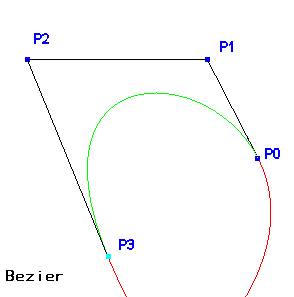 Les segments
de droite en noir qui relient les Pi s'appellent le Polygone de contrôle.
Les segments
de droite en noir qui relient les Pi s'appellent le Polygone de contrôle.